TEXTO DO EP-107-QB-70-O CÓDIGO DOS GASES: DECIFRANDO LEIS E TRANSFORMAÇÕES

Sejam todos muito bem-vindos a mais um episódio do Papo de Química e hoje vamos mergulhar no fascinante universo dos gases. Apesar de invisíveis, os gases estão em tudo que a gente faz, desde respirar até acender uma chama no fogão. Vem com a gente porque hoje vamos decifrar o código dos gases, entendendo como pressão, volume, temperatura e quantidade de matéria moldam o nosso mundo. Vamos começar pelo básico: as variáveis de estado. São elas que descrevem um gás: pressão (P), volume (V), temperatura (T) e quantidade de matéria (n).  Pensa assim: é como se fosse a “ficha de identidade” do gás. Se eu sei essas quatro variáveis, consigo prever o comportamento dele. Exemplo prático: o ar dentro de um pneu. Ele tem um volume fixo, mas a pressão muda quando a temperatura aumenta, como num dia quente.

Quando uma dessas variáveis permanece constante e as outras mudam, temos as transformações gasosas. Existem três tipos principais: isotérmica (T constante), isobárica (P constante) e isocórica ou isovolumétrica (V constante). E claro, existe a equação geral dos gases, que une todas elas num só modelo.

Na transformação isotérmica, a temperatura do gás permanece constante durante todo o processo. Quando falamos de um gás ideal, isso significa que a pressão e o volume estão ligados de forma inversa:

• Se o volume diminui, a pressão aumenta.

• Se o volume aumenta, a pressão diminui.

Essa relação é descrita pela conhecida Lei de Boyle-Mariotte.

Imagine uma seringa (sem agulha).Se você empurra o êmbolo, o espaço interno diminui- o volume do ar fica menor.  O que acontece? Você sente resistência ! Isso é a pressão aumentando. Agora, se você puxa o êmbolo, o volume aumenta e a pressão diminui, ficando mais fácil de puxar. Essa é uma demonstração prática da relação entre pressão e volume numa transformação isotérmica.

Matematicamente, isso se expressa assim :  P ∝ 1/V , ou seja,  P × V = constante

Isso quer dizer que, em qualquer ponto do processo, o produto entre pressão e volume será sempre o mesmo. Comparando dois momentos diferentes, usamos a fórmula:

 P₁ × V₁ = P₂ × V₂

Onde:

• P₁ e V₁ são a pressão e o volume no início.
• P₂ e V₂ são a pressão e o volume em outro momento qualquer.

Se colocarmos isso num gráfico de pressão (P) no eixo vertical e volume (V) no eixo horizontal, veremos uma hipérbole- uma curva que mostra a relação inversa entre as grandezas.

Vamos a um exemplo: Um gás ocupa 4 L a 2 atm de pressão. Qual será o volume se a pressão cair para 1 atm?

Aplicando a Lei de Boyle : P₁V₁ = P₂V₂    \ 2 atm x 4L = 1 atm x V₂ ⇒V₂ = 8 L

Na transformação isobárica o volume e temperatura mudam, mas a pressão se mantem constante. Essa é a Lei de Charles e Gay-Lussac. Ela diz que o volume é diretamente proporcional à temperatura absoluta (medida em Kelvin).

• Se a temperatura aumenta, o volume também aumenta.
• Se a temperatura diminui, o volume se reduz.

A relação entre volume e temperatura pode ser representada por:

V ∝ T ⇒   =constante

Quando comparamos dois estados diferentes:     V1/T1 =V2/T2

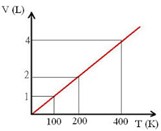
O gráfico V × T é uma reta crescente que passa pela origem. 

Por que balões de gás incham ao sol? Porque o ar interno aquece em seu interior aquece. Com a temperatura mais alta, o volume aumenta. Um exemplo direto da Lei de Charles em ação!

Vamos a um problema: Um gás ocupa um volume de 2,0 L a 27 °C. Qual será o novo volume quando a temperatura for elevada para 327 °C, mantendo-se a pressão constante?

Dados:

• Volume inicial (V₁): 2,0 L
• Temperatura inicial (T₁): 27 °C = 27 + 273 = 300 K
• Temperatura final (T₂): 327 °C = 327 + 273 = 600 K
• Volume final (V₂): ?

Aplicando a     V1/T1 = V2/T2         \   Substituindo os valores:  2/300 = V2/600 

Resolver com regra de três ou Multiplicação cruzada:        V2= 4L

Na transformação isocórica (ou isovolumétrica), o volume não muda. O que varia com a temperatura é a pressão. Pela Lei de Gay-Lussac, a pressão é diretamente proporcional à temperatura absoluta (em Kelvin). Isso significa que, quando a temperatura do gás aumenta, sua pressão também aumenta na mesma proporção, e quando a temperatura diminui, a pressão se reduz.

Matematicamente :  P ∝ T  ⇒    = constante

onde K é uma constante característica para a massa fixa de gás mantida em volume constante.

Quando comparamos dois estados diferentes:   P1/T1=P2/T2 

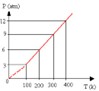
O gráfico P × T: também é uma reta crescente passando pela origem 

Exemplo: uma lata de spray deixada no sol. A temperatura sobe, a pressão interna aumenta, e pode causar uma explosão.

Um gás ideal está contido em um recipiente rígido (volume constante). Inicialmente, encontra-se a  P₁=2,0 atm e T₁=300 K. O sistema é aquecido até T₂ = 450 K, sem variação de volume e de quantidade de matéria. Determine a pressão final P₂ do gás. 

Dados: P₁=2,0 atm ;  T₁=300 K ; T₂=450 K , P₂=? 

Aplicando a Lei de Gay-Lussac :   P1/T1 = P2/T2 

Substituindo os valores:   2/300 = P2/450                

Resolver com regra de três ou Multiplicação cruzada:   P2 = 3 atm

Quando pressão (P), volume (V) e temperatura (T) mudam ao mesmo tempo, usamos, usamos a equação geral dos gases : P1xV1/T1  = P2xV2/T2

• P₁​,V₁​,T₁​: valores iniciais de pressão, volume e temperatura
• P₂,V₂,T₂: valores finais após a mudança de estado
• n (número de mols) permanece constante
• T deve estar em Kelvin

Um gás ocupa 5 L sob pressão de 2 atm e temperatura de 300 K.
Qual será o volume ocupado por esse gás se a pressão for reduzida para 1 atm e a temperatura aumentada para 600 K?

Dados do problema

• P₁=2 atm
• V₁=5 L
• T₁=300 K
• P₂=1 atm
• T₂=600 K
• V₂=?

Como a quantidade de matéria (n) é constante, usamos:   P1.V1/T1  = P2.V2/T2 

Substituindo os valores: 2x5/300 = 1xV2/400       V2= 20L

Hoje vimos como leis formuladas há séculos ainda explicam fenômenos do nosso dia-a-dia- dos pneus ao clima, dos balões a indústria. E aprendemos que os gases seguem padrões previsíveis e calculáveis. A Ciência está em toda parte!