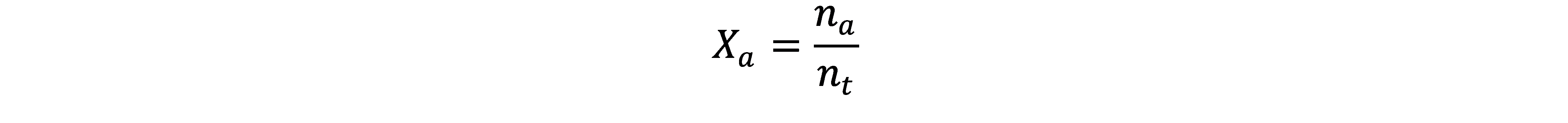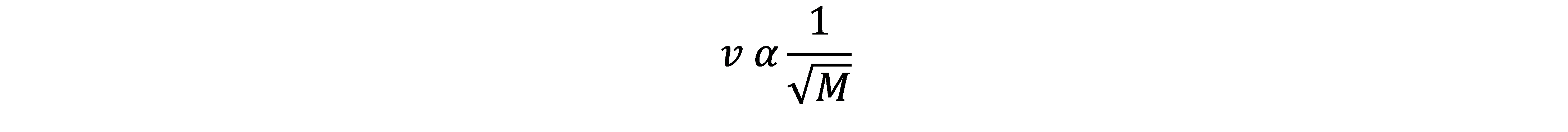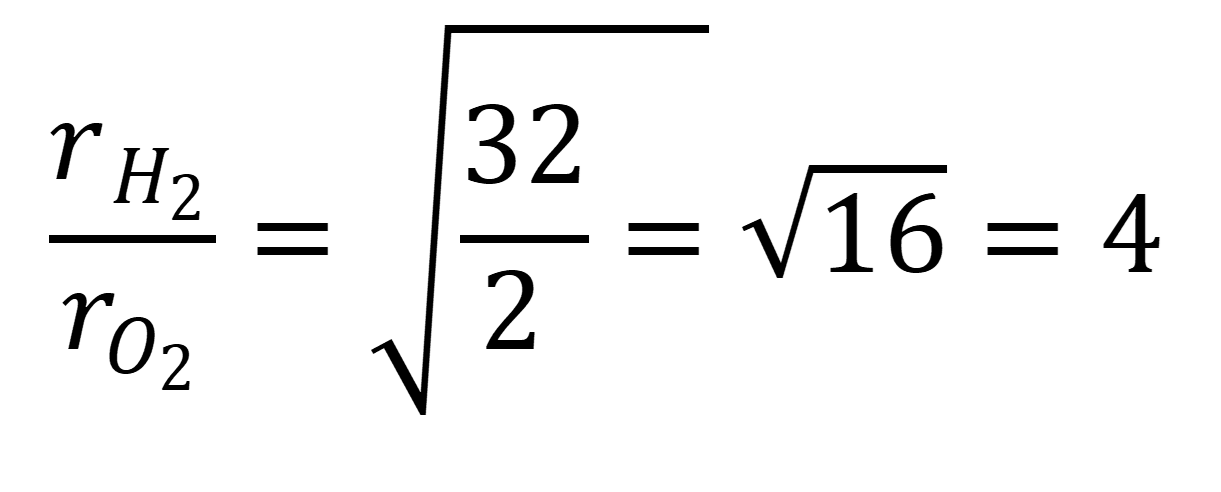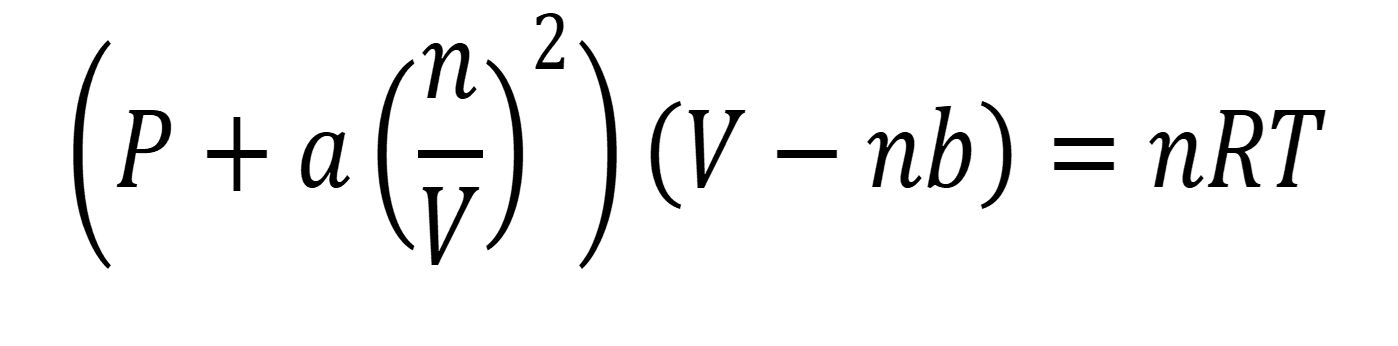TEXTO-EP-108-“GASES EM AÇÃO : O SHOW DAS MOLÉCULAS”

Esse é o terceiro episódio da nossa série sobre o estudo dos gases!  Se você ainda não ouviu os episódios 106 e 107, corre lá na sua plataforma favorita de áudio. e escuta — eles são essenciais pra entender essa jornada gasosa do começo ao fim! Vamos começar com uma recapitulação rapidinha. Quando a gente mantém a quantidade de matéria constante, aquela letrinha "n", e varia pressão, volume e temperatura, a gente usa a equação:     

   , P e V são pressão e volume, T é a temperatura — sempre em Kelvin! E os subscritos 1 e 2 representam os estados inicial e final.   Mas... e quando todas essas variáveis mudam juntas e a gente quer saber a quantidade de gás, por exemplo? Aí entra a estrela do dia: a equação de Clapeyron!

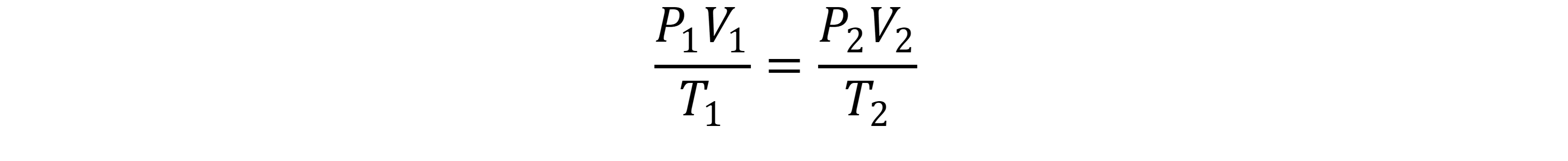
A equação é simples e poderosa:  PV = nRT  , Onde: P é pressão (em atm), V é volume (em litros), n é o número de mols, T é a temperatura (em Kelvin), e R é a constante universal dos gases. Aliás, R pode ter diferentes valores dependendo da unidade usada, mas no geral a gente usa: R = 0,082 atm·L·mol⁻¹·K⁻¹

Vamos pra um exemplo prático!  Imagina que você tem 5,0 L de gás oxigênio, a 300 K e sob pressão de 2,5 atm. Quanto isso dá em mols e em massa?

A partir da equação de Clapeyron,  usamos a equação: n = PV / RT, substituindo os valores   n = (2,5 × 5,0) / (0,082 × 300) = 0,508 mol

E como a massa molar do oxigênio(O₂) é 32 g/mol, a massa será:  m = n × M = 0,508 × 32 = 16,3 g

Falando em mols, você sabia que 1 mol de gás ideal ocupa 22,4 litros em CNTP?

Sim! CNTP é o padrão que usamos aqui no Brasil — 0 °C e 1 atm. Já as condições de Pressão e Temperatura padrão(STP), usado pela IUPAC, considera 1 bar de pressão.

E por isso, em STP, o volume molar ideal é 22,7 L/mol. Quase igual, mas com aquela diferença nerd que a gente ama!

Você sabia que dá pra calcular a densidade de um gás a partir da equação de Clapeyron?

Tudo começa com a equação: PV = nRT ,  agora, lembrando que o número de mols (n) pode ser escrito como a razão entre a massa (m) e a massa molar (M), ou seja:    n = m/M

Substituindo isso na equação de Clapeyron, temos: PV = (m/M)RT

Reorganizando a equação, podemos isolar a densidade. Como densidade é massa por volume, ou seja, d = m/V, chegamos à expressão:

d = PM / RT

Essa fórmula nos mostra que a densidade de um gás depende da pressão (P), da massa molar (M), da temperatura (T) e da constante dos gases (R). Uma forma prática e poderosa de entender o comportamento dos gases em diferentes condições!

Vamos a um exemplo prático?  Qual é a densidade do gás oxigênio (O₂) sob pressão de 1,10 atm e temperatura de 35 °C?

Passo 1: Converter a temperatura para Kelvin

Lembrando que a temperatura na equação dos gases deve estar em Kelvin:
T = 35 + 273 = 308 K

Passo 2: Aplicar a fórmula da densidade

A equação é:  d = (P × M) / (R × T)

Onde:

• P = 1,10 atm
• M = 32 g/mol (massa molar do O₂)
• R = 0,082 atm·L/mol·K
• T = 308 K 

Substituindo os valores: d = (1,10 × 32) / (0,082 × 308)

d ≈ 35,2 / 25,26  

d ≈ 1,39 g/L

E dá pra fazer o caminho inverso também! Se souber a densidade, a pressão e a temperatura, dá pra calcular a massa molar do gás. 

A Lei de Avogadro é linda: mesmo volume, mesma temperatura e mesma pressão → mesmo número de partículas, não importa o gás!

Isso mesmo! Por isso, 1 L de H₂ tem o mesmo número de moléculas que 1 L de O₂ em CNTP:

6,02 × 10²³ moléculas!

E se dobrar o número de mols, dobra o volume também! A equação é: V₁/n₁ = V₂/n₂

Agora vamos de Lei de Dalton! Em uma mistura de gases, a pressão total é a soma das pressões parciais:

P_total = P₁ + P₂ + ...P_n

Quer um exemplo? Aqui vai:

Temos uma mistura gasosa formada por dois gases:

• Oxigênio (O₂) a 0,8 atm
• Nitrogênio (N₂) a 0,2 atm

Qual é a pressão total da mistura?

Segundo a Lei de Dalton, a pressão total de uma mistura gasosa é a soma das pressões parciais de cada gás presente. Em outras palavras:

P_total = P_O₂ + P_N₂

Substituindo os valores: P_total = 0,8 atm + 0,2 atm =igma( 1,0 atm

 E dá pra calcular a pressão parcial com fração molar também:    , lembrando que 

Temos um frasco com volume V e temperatura T constantes. No seu interior, há uma mistura gasosa com:

• 0,60 mol de N₂
• 0,40 mol de O₂
• Pressão total da mistura: 1,20 atm

Queremos calcular:  As pressões parciais do N₂ e do O₂.

 Passo 1: Calcular a fração molar de cada gás

A fórmula da fração molar (X) é:     Xₐ = nₐ / n_total 

• n_total = 0,60 + 0,40 = 1,00 mol
• X_N₂ = 0,60 / 1,00 = 0,60
• X_O₂ = 0,40 / 1,00 = 0,40  

Passo 2: Aplicar a fórmula da pressão parcial

A fórmula é:   Pₐ = P_total × Xₐ

• P_N₂ = 1,20 atm × 0,60 = 0,72 atm
• P_O₂ = 1,20 atm × 0,40 = 0,48 atm

Resultado final:

Pressão parcial do N₂: 0,72 atm

Pressão parcial do O₂: 0,48 atm

E, claro: 0,72 + 0,48 = 1,20 atm → Confirmando a pressão total!

A Lei de Amagat afirma que, para uma mistura gasosa nas mesmas temperatura (T) e pressão (P), o volume total é igual à soma dos volumes parciais que cada componente ocuparia se estivesse isolado nas mesmas condições.

Quando a Lei é Válida?

• Exata para misturas ideais, sob baixa pressão e comportamento ideal.

• Aproximação para gases reais — pode falhar em pressões elevadas ou quando há fortes interações entre moléculas.

 Quer um exemplo? Aqui vai:

Considere 40 L de uma mistura formada por 1mol de CO₂ e 3 mols de N₂ , em condições fixas de T e P. Calcule o volume de cada gás

1) Vamos calcular a fração molar de cada gás

• X_CO2=1/1+3 = ¼ = 0,25
• X_N2=3/4 = 0,75  

2) Cálculo do volume de cada gás

V_CO2 = 40 × 1/4=10 L

V_N2 = 40 × 3/4=30 L

A Lei de Graham estabelece que a velocidade de difusão ou efusão de um gás é inversamente proporcional à raiz quadrada de sua massa molar.

Em outras palavras:

Gases mais leves (com menor massa molar) se difundem ou efundem mais rapidamente do que gases mais pesados, quando estão sob as mesmas condições de temperatura e pressão.

• Forma matemática (para dois gases 1 e 2):   

onde r é a taxa de difusão/efusão e M é a massa molar.

Vamos comparar as velocidades de efusão do hidrogênio (H₂) e do oxigênio (O₂).

• Massa molar de H₂ ≈ 2 g/mol
• Massa molar de O₂ ≈ 32 g/mol

 Aplicando a Lei de Graham:

Logo, o hidrogênio difunde/eflui cerca de 4 vezes mais rápido que o oxigênio.

Claro que nem tudo são flores. O modelo de gás ideal funciona bem em baixas pressões e altas temperaturas...

Mas começa a falhar quando as moléculas se aproximam demais — surgem interações, e o volume delas não pode ser ignorado.

Aí entra a equação de van der Waals, com correções para pressão (a) e volume (b):

Quando a = 0 e b = 0, ela vira o nosso velho conhecido PV = nRT. Mas quando as condições apertam, ela mostra como os gases se comportam de verdade.

Ufa! Hoje foi gás do começo ao fim! Mas olha quanto conteúdo incrível a gente viu!

De Clapeyron a Graham, passando por densidade, volume molar, leis de mistura... um verdadeiro show das moléculas!

E semana que vem tem mais! Então já segue a gente no seu tocador favorito e compartilha com aquele amigo que vive dizendo: “Ah, química é difícil…” — manda esse episódio pra ele!

Até a próxima!